前提知識
他の複雑性クラスについては、以下もご覧ください。
クラス$\textrm{NP}$というものがあります。これは、YESである証拠が与えられた時、多項式時間でその正しさを検証できるクラスでした。つまり、一つでもYESである証拠が見つかれば、その問題はYESであるということです。
しかし、その問題がNOである場合、特定のアルゴリズムが存在しなければ、すべての証拠を検証して、すべて非受理であったと確認する必要があります。しかし、その時間は、多項式時間で収める必要がありません。
例えば、充足可能性問題(SAT)は、「論理式全体の値を真にするような、変数への真偽割り当てが存在する」かどうかを判定する問題です。
この問題は、論理式全体が真となる変数の真偽割り当てを実際に論理式に代入してみると、多項式時間で検証できるので、$\textrm{NP}$に属する問題です。
しかし、論理式全体が偽となる割り当てを一つ代入しても、充足可能な組み合わせが存在しない証明にはなりません。
つまり、ある決定問題のYES/NOを入れ替えただけの問題でも、難しさが違う可能性がある(後で説明します)ということです。
補問題
クラス$\textrm{co-P}$や$\textrm{co-NP}$の定義の前に、補問題という用語を定義しておきます。
補問題とは、決定問題のYES/NOが逆になった問題のことです。
例えば、先ほどの例のように、SATでは、割り当てが存在するならYESを(存在しないならNOを)出力しましたが、SATの補問題では、割り当てが存在しないならYESを(存在するならNOを)出力する問題です1。
$\textrm{co-P}$
$\textrm{co-P}$の定義
ある決定問題Sが$\textrm{co-P}$に属するとは、Sの補問題が$\textrm{P}$に属する問題であることを言います。
つまり、$\textrm{co-P}$とは、$\textrm{P}$に属する問題の補問題が属するクラスとも言えます。
$\textrm{P}=\textrm{co-P}$
$\textrm{co-P}$は$\textrm{P}$と同じです。言い換えると、$\textrm{P}$に属する問題の補問題は、$\textrm{P}$に属します。
これは、$\textrm{P}$に属する問題Sを解く決定性チューリングマシンMの受理/非受理状態を入れ替えたマシンM’を作り、それを用いて解けばいいからです。なお、動作関数にない入力があった場合は、即「受理」とします(元のマシンでは即「不受理」)。
では、これを同じように非決定性チューリングマシンで行うと、$\textrm{NP}=\textrm{co-NP}$も簡単に証明できるのではないかと考えるのが自然ですが、実はこれはできません。後ほど説明します。
$\textrm{co-NP}$
$\textrm{co-NP}$の定義
ある決定問題Sが$\textrm{co-NP}$に属するとは、Sの補問題が$\textrm{NP}$に属する問題であることを言います。
つまり、$\textrm{co-NP}$とは、$\textrm{NP}$に属する問題の補問題が属するクラスとも言えます。
ほかの複雑性クラスとの関係
クラス$\textrm{P}$との関係
$\textrm{P}\subseteq \textrm{co-NP}$です。
$\textrm{P}\subseteq \textrm{NP}$なので、$\textrm{co-P}\subseteq \textrm{co-NP}$であり、さらに$\textrm{P}=\textrm{co-P}$だからです。
クラス$\textrm{NP}$との関係
$\textrm{co-NP}$を考えるにあたって、やはり気になるのは、$\textrm{co-NP}$に属する問題は、$\textrm{NP}$に属する問題より簡単なのか、難しいのか、ということだと思います。
先ほどの例を見ると、$\textrm{co-NP}$に属する問題のほうが明らかに難しそうに感じます2が、実は未解決です。
なぜ$\textrm{P}=\textrm{co-P}$のようにはできないのか
決定性チューリングマシンと非決定性チューリングマシンで一体何が違うのか、と思われるかもしれませんが、非決定性チューリングマシンでは、同じ入力に対して複数の遷移先が存在することがある、という点に注意してください。
つまり、非決定性チューリングマシンでは、ある入力に対して、受理/非受理の複数の最終状態が存在する可能性があり、このとき一つでも受理状態であれば「受理」とします。
ここで、以下のような非決定性チューリングマシンMを考えてみましょう。
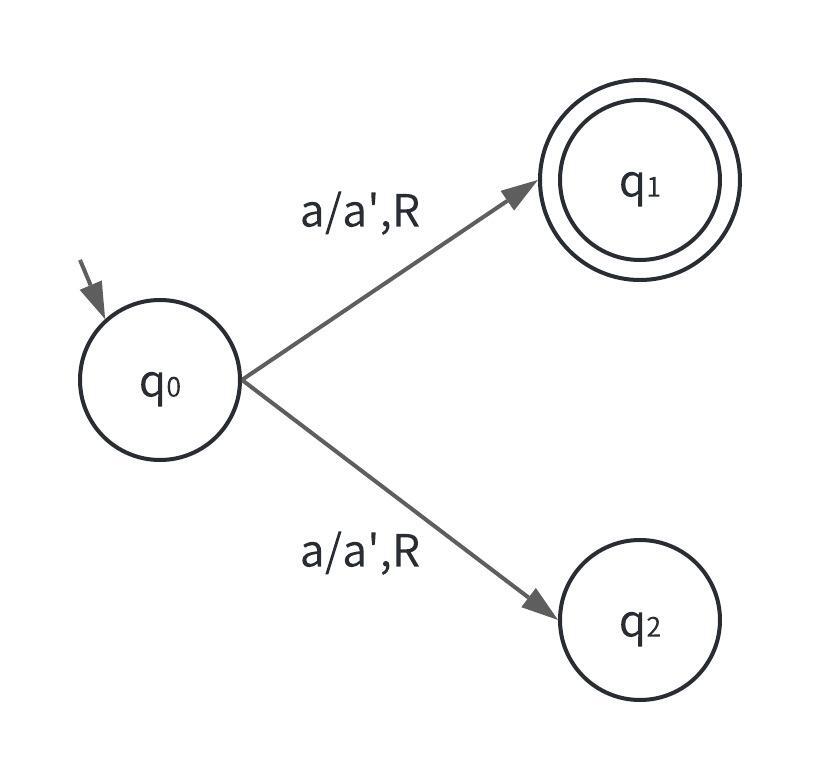
Mに$a$という語を入力すると、$q_{1}$と$q_{2}$の両方に達し、$q_{1}$は受理状態なので、マシンは「受理」を返します。
Mの受理/非受理を、$\textrm{P}=\textrm{co-P}$の証明と同様に逆転させたマシンM’を考えると、以下になります。
なお、今回は$a$以外の入力の遷移先は省きます。
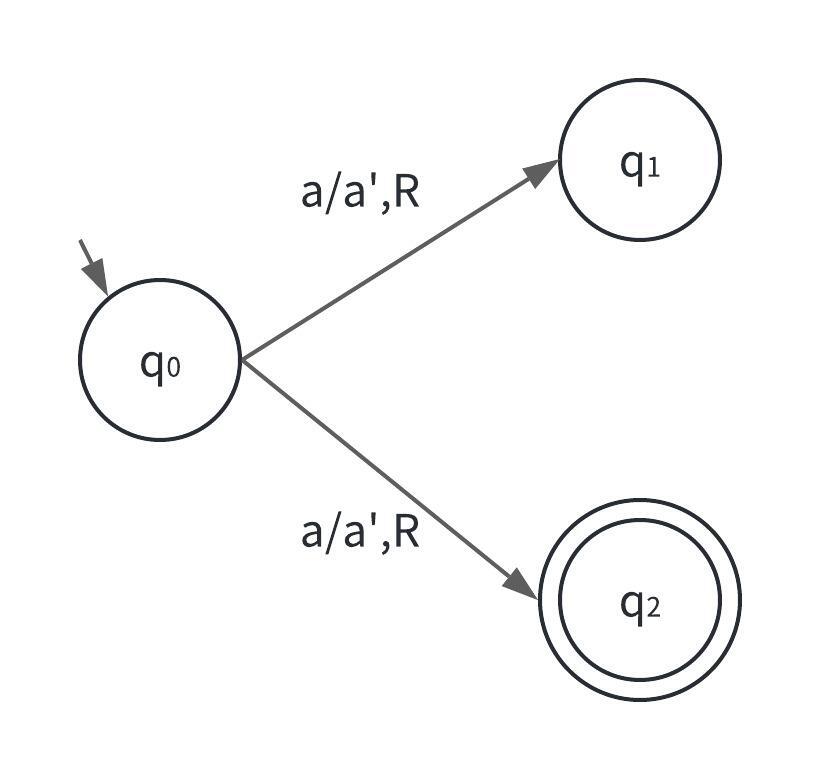
補問題なので、非受理でなければいけないですが、$q_{2}$で受理されてしまいました。
以上より、この証明方法は失敗です。
逆に、$\textrm{P}=\textrm{co-P}$の証明では、各ステップの遷移先が1つに限定されていたから上手くいったのです。
参考:$\textrm{P}=\textrm{NP}$の場合
ただし、$\textrm{P}=\textrm{NP}$を仮定すると、$\textrm{NP}=\textrm{co-NP}$です。
$\textrm{P}=\textrm{NP}$より、$\textrm{P}$の補問題が属するクラス3が$\textrm{co-NP}$となります。
つまり、仮定の下では、クラス$\textrm{co-NP}$はクラス$\textrm{co-P}$ということです。
ここで、$\textrm{P}=\textrm{co-P}$を思い出すと、$\textrm{NP}=\textrm{P}=\textrm{co-P}=\textrm{co-NP}$と等号で結べて、$\textrm{NP}=\textrm{co-NP}$となります。
つまり、
\begin{align*}
\textrm{P}=\textrm{NP}\Rightarrow \textrm{NP}=\textrm{co-NP}
\end{align*}
です4。
$\textrm{P}=(\textrm{NP}\cap\textrm{co-NP})$か?
$\textrm{NP}$かつ$\textrm{co-NP}$である問題が、$\textrm{P}$に属する問題以外に存在するかは、未解決です。
$\textrm{P}\subseteq (\textrm{NP}\cap\textrm{co-NP})$である
$\textrm{P}\subseteq \textrm{NP} \land \textrm{P}\subseteq \textrm{co-NP}$なので、$\textrm{P}\subseteq (\textrm{NP}\cap\textrm{co-NP})$が成り立ちます。
$\textrm{P}\supseteq (\textrm{NP}\cap\textrm{co-NP})$かどうかは未解決
ただし、$\textrm{P}=\textrm{NP}$を仮定すると、$\textrm{NP}=\textrm{co-NP}$であったから、$\textrm{P}= (\textrm{NP}\cap\textrm{co-NP})$が成立します。
$\textrm{P}\ne\textrm{NP}$の場合はわかりません。
こう見ると、$\textrm{P}=\textrm{NP}$問題の位置づけってとんでもないんですね。
コメント